Original: http://www.math.stonybrook.edu/~tony/mazes/satmaze.html

Labirintusokon keresztül a matematikáig

A legismertebb ilyen útvesztő a krétai labirintus. Rajzolható játékként.

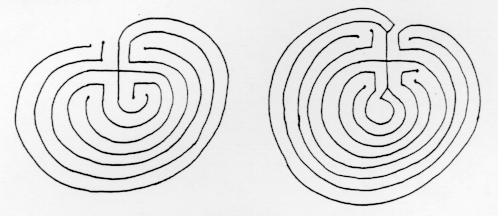
Itt van egy másik példa. Ez az útvesztő több középkori héber kéziratban jelenik meg. Bár ez az útvesztő felszínesen hasonlít a krétai útvesztőhöz, egy szoros összehasonlítás azt mutatja, hogy egészen mások. A Jericho labirintusnak 7 szintje van, míg a krétai labirintusnak 8 szintje van, és a szintek elérésének sorrendje labirintusonként eltér. Mindkét labirintusban az út közvetlenül a 3. szintre megy (a külsőt 0-nak számítva), de a krétai labirintusban ezután a duplájára duplázik a 2. és az 1. szintre, míg a jerikói labirintusban a 4. és az 5. szinten halad tovább, mielőtt visszatérne a 2. és 1. A teljes szinten szekvenciák vannak

Cretan 032147658

Jericho 03452167.

Azokat a tulajdonságokat, amelyekkel e két útvesztő osztozik, és amelyek egy egyszerű matematikai leírással rendelkező útvesztők osztályának meghatározására szolgálnak, összefoglalhatjuk úgy, hogy egyszerű, váltakozó útvesztőknek (s.a.t. útvesztőknek) nevezzük őket.

TRANZIT labirintusok, mert az út kétirányú elágazás nélkül fut az útvesztő külsejétől a középpontig. Például ezek a labirintusok nem átmenő útvesztők: az egyikben az út ugyanazon az oldalon jön ki, ahová belépett; a másikban pedig vannak olyan pontok, ahol a labirintus futójának választania kell, hogy melyik utat választja.

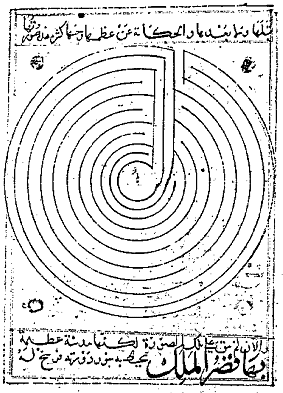
ALTERNATÍV, mert a labirintus terve bizonyos számú koncentrikus vagy párhuzamos szintre van felrajzolva, és a labirintus útvonala változik, ha szintet vált. Például ennek a labirintusnak, amely egy középkori arab földrajzi könyvben Konstantinápoly tervét ábrázolja, külön szintjei vannak, de nem váltakoznak, mivel a 10. szintről az 1. szintre fordul, irányváltás nélkül. A 0.3.4.5.6.7.8.9.10.1.2.11 szintű szekvenciája nem fordulhat elő, mint látni fogjuk, mint egy váltakozó labirintus szintje.

EGYSZERŰ, mert az út lényegében egy teljes kört alkot minden szinten; különösen minden szinten pontosan egyszer utazik. Például ez a váltakozó útvesztő labirintus, amely Chartres-ban (itt látható) és számos más katedrálisban járda útvesztőként fordul elő, és a luccai székesegyház oszlopára van faragva, nem egyszerű: négy különböző pont van, ahol az út szintet változtathat. Úgy tűnik, hogy ez a labirintus-minta a krétai rajzolat és a római leszármazottak keresztény kidolgozásaként és felerősítéseként történt; fennmaradt az asszociáció a Theseus-mítosszal. Az új kialakítás maga is rendkívül kitartó volt. A 9. századból származó középkori kéziratokban látható; A Chartres-székesegyház 1200 körül épült; és a 16. század elején azonos mintát festettek egy florentin kasszonra. Most háromdimenziósan renderelték, páncélos Theseus a Minotaurusz ellen küzdött a közepén.

Az egyszerű, váltakozó tranzit labirintus TOPOLÓGIÁJÁT teljesen meghatározza annak szintje.

Tony Phillips
Matematika Tanszék SUNY Stony Brook
tony at math.stonybrook.edu
2020. szeptember 30